Trong chương trình Toán học lớp 7, việc chứng minh hai đường thẳng song song là một kỹ năng quan trọng mà học sinh cần nắm vững. Blog Làm Cha sẽ giúp các em hiểu rõ và thực hành tốt phần kiến thức này thông qua bài viết chi tiết dưới đây.
Kiến thức cơ bản về đường thẳng song song
Định nghĩa đường thẳng song song
Hai đường thẳng được gọi là song song với nhau khi chúng nằm trong cùng một mặt phẳng và không có điểm chung. Kí hiệu hai đường thẳng a và b song song là: a // b.
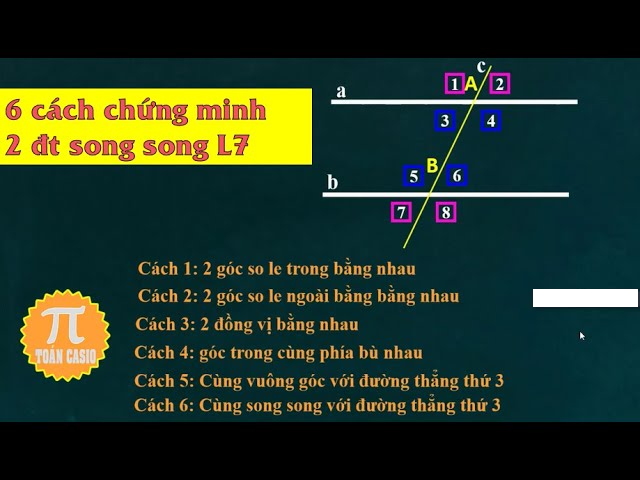
Các dấu hiệu nhận biết hai đường thẳng song song
- Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba
- Khoảng cách giữa hai đường thẳng luôn không đổi
- Hai đường thẳng không giao nhau dù kéo dài vô hạn
Các định lý quan trọng về đường thẳng song song
Định lý về góc đồng vị
Khi một đường thẳng cắt hai đường thẳng khác tạo thành các góc đồng vị bằng nhau thì hai đường thẳng đó song song với nhau.
Ví dụ:
- Nếu hai góc trong cùng phía bằng nhau
- Nếu hai góc ngoài cùng phía bằng nhau
- Nếu hai góc so le bằng nhau
Định lý về góc đối đỉnh
Khi một đường thẳng cắt hai đường thẳng khác:
- Các góc đối đỉnh bằng nhau
- Tổng các góc trong cùng phía bằng 180°
- Tổng các góc ngoài cùng phía bằng 180°

Các bước chứng minh hai đường thẳng song song
Phương pháp 1: Sử dụng góc đồng vị
- Xác định đường cắt (đường thẳng cắt cả hai đường cần chứng minh)
- Tìm các cặp góc đồng vị
- Chứng minh các góc đồng vị bằng nhau
- Kết luận hai đường thẳng song song
Ví dụ minh họa: Cho hai đường thẳng a và b bị cắt bởi đường thẳng c. Nếu góc trong cùng phía α = 120° và góc trong cùng phía β = 120°, chứng minh a // b.
Lời giải:
- Ta có: α = β = 120° (theo giả thiết)
- α và β là góc trong cùng phía
- Theo định lý: Khi góc trong cùng phía bằng nhau thì hai đường thẳng song song
- Vậy: a // b
Xem thêm Hướng Dẫn Chi Tiết Công Thức Tính Diện Tích Xung Quanh Cho Con
Phương pháp 2: Sử dụng góc so le
- Xác định đường cắt
- Tìm các cặp góc so le
- Chứng minh các góc so le bằng nhau
- Kết luận hai đường thẳng song song
Phương pháp 3: Sử dụng tổng các góc
- Xác định đường cắt
- Tìm tổng các góc trong cùng phía hoặc ngoài cùng phía
- Chứng minh tổng bằng 180°
- Kết luận hai đường thẳng song song
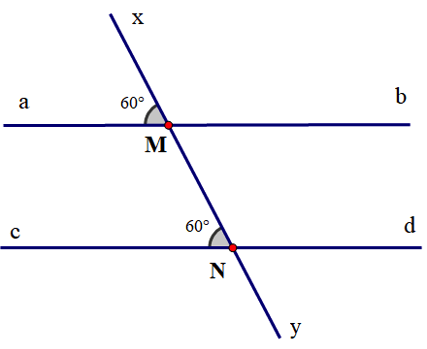
Các bài tập thường gặp và cách giải
Bài tập mẫu 1
Cho hai đường thẳng a và b bị cắt bởi đường thẳng c tại A và B. Biết góc trong cùng phía α = 70° và góc kề với nó là 110°. Chứng minh a // b.
Lời giải:
- Ta có góc kề với α là 110°
- Tổng hai góc kề bù = 180°
- Góc trong cùng phía β = 70° (vì 180° – 110° = 70°)
- Do α = β = 70° là hai góc trong cùng phía
- Theo định lý về góc trong cùng phía
- Kết luận: a // b
Bài tập mẫu 2
Cho hai đường thẳng a và b bị cắt bởi đường thẳng c. Biết góc so le α = 125° và góc so le β = 125°. Chứng minh a // b.
Lời giải:
- Ta có α = β = 125° (góc so le)
- Theo định lý về góc so le
- Kết luận: a // b
Xem thêm Câu Đố Vui Trẻ Em: Kho Tàng Trí Tuệ Đầy Màu Sắc
Các lỗi thường gặp khi chứng minh
Lỗi về xác định góc
- Nhầm lẫn giữa các loại góc:
- Góc đồng vị
- Góc so le
- Góc đối đỉnh
- Cách khắc phục:
- Vẽ hình rõ ràng
- Đánh dấu các góc cẩn thận
- Kiểm tra kỹ định nghĩa của từng loại góc

Lỗi về lập luận
- Thiếu các bước chứng minh
- Không nêu rõ định lý sử dụng
- Kết luận không đầy đủ
Lời khuyên khi học và làm bài
Cách học hiệu quả
- Nắm vững định nghĩa và các định lý
- Luyện tập nhiều dạng bài tập
- Vẽ hình cẩn thận, rõ ràng
- Ghi chép đầy đủ các bước chứng minh
Cách làm bài kiểm tra
- Đọc kỹ đề bài
- Vẽ hình minh họa
- Lập luận theo các bước:
- Giả thiết
- Chứng minh
- Kết luận
- Kiểm tra lại bài làm
Kết luận
Chứng minh hai đường thẳng song song là một kỹ năng quan trọng trong chương trình Toán học lớp 7. Để thành thạo kỹ năng này, các em cần:
- Nắm vững kiến thức cơ bản
- Hiểu rõ các định lý
- Thực hành nhiều bài tập
- Rèn luyện tư duy logic
Để được hỗ trợ thêm về cách chứng minh hai đường thẳng song song cũng như các kiến thức Toán học khác, phụ huynh và học sinh có thể liên hệ với Blog Làm Cha qua:
- Hotline: 0903 323 444
- Email: [email protected]
- Website: bloglamcha.com
Blog Làm Cha luôn sẵn sàng đồng hành cùng các em trong việc học tập và phát triển kiến thức toán học.

No Responses