Xin chào quý phụ huynh và các em học sinh thân mến của Blog Làm Cha! Hôm nay, chúng ta sẽ cùng tìm hiểu về một chủ đề quan trọng trong chương trình Toán học lớp 10: các công thức tính diện tích tam giác. Bài viết này sẽ giúp các em nắm vững kiến thức và áp dụng hiệu quả trong việc giải các bài toán liên quan.
Những Kiến Thức Cơ Bản Về Tam Giác
Định Nghĩa và Tính Chất
- Tam giác là đa giác có ba cạnh, ba đỉnh và ba góc
- Tổng các góc trong tam giác bằng 180 độ
- Độ dài mỗi cạnh nhỏ hơn tổng hai cạnh còn lại
- Các yếu tố cơ bản:
- Ba cạnh: a, b, c
- Ba góc: A, B, C
- Ba đường cao: ha, hb, hc
- Diện tích: S

Phân Loại Tam Giác
- Theo góc:
- Tam giác vuông (có một góc 90 độ)
- Tam giác nhọn (ba góc nhọn)
- Tam giác tù (có một góc lớn hơn 90 độ)
- Theo cạnh:
- Tam giác đều (ba cạnh bằng nhau)
- Tam giác cân (hai cạnh bằng nhau)
- Tam giác thường (ba cạnh không bằng nhau)
Các Công Thức Tính Diện Tích Tam Giác Cơ Bản
Công Thức Cạnh và Đường Cao
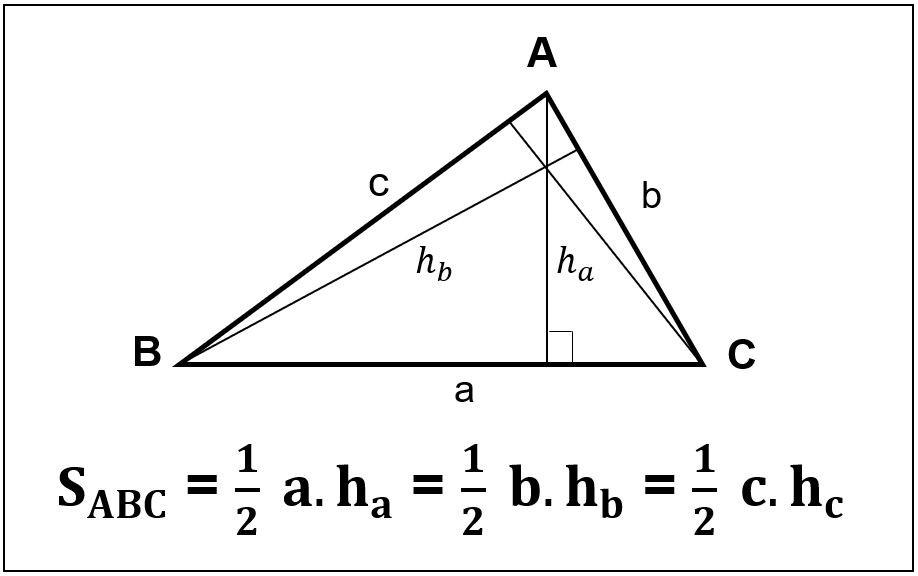
- Công thức tổng quát:
- S = (1/2) × a × ha
- S = (1/2) × b × hb
- S = (1/2) × c × hc Trong đó:
- S là diện tích tam giác
- a, b, c là độ dài các cạnh
- ha, hb, hc là độ dài các đường cao tương ứng
- Ưu điểm và nhược điểm:
- Ưu điểm: Dễ nhớ, dễ áp dụng
- Nhược điểm: Cần biết đường cao
Công Thức Heron
- Công thức:
- S = √(p(p-a)(p-b)(p-c)) Trong đó:
- p = (a + b + c)/2 (nửa chu vi)
- a, b, c là độ dài các cạnh
- Ứng dụng:
- Thích hợp khi biết ba cạnh
- Không cần thông tin về góc hay đường cao
Các Công Thức Tính Diện Tích Tam Giác Nâng Cao
Công Thức Lượng Giác
- Sử dụng hàm sin:
- S = (1/2) × a × b × sin(C)
- S = (1/2) × b × c × sin(A)
- S = (1/2) × a × c × sin(B)
- Ưu điểm:
- Hữu ích khi biết hai cạnh và góc xen giữa
- Dễ áp dụng trong tam giác vuông
Xem thêm Hướng Dẫn Chi Tiết: Hàm Số Đồng Biến Nghịch Biến Lớp 10
Công Thức Bán Kính
- Với bán kính đường tròn ngoại tiếp (R):
- S = abc/(4R)
- Với bán kính đường tròn nội tiếp (r):
- S = p × r Trong đó p là nửa chu vi
Phương Pháp Giải Bài Tập
Các Bước Giải Cơ Bản
- Phân tích đề bài:
- Xác định các yếu tố đã cho
- Xác định yếu tố cần tìm
- Lựa chọn công thức:
- Dựa vào dữ kiện đã cho
- Chọn công thức phù hợp nhất
- Giải bài toán:
- Áp dụng công thức đã chọn
- Tính toán cẩn thận

Ví Dụ Minh Họa
- Bài toán 1:
- Cho tam giác ABC có cạnh a = 3cm, b = 4cm, c = 5cm. Tính diện tích tam giác. Giải:
- Áp dụng công thức Heron
- p = (3 + 4 + 5)/2 = 6
- S = √(6(6-3)(6-4)(6-5)) = 6 (cm²)
- Bài toán 2:
- Cho tam giác vuông ABC có cạnh đáy a = 6cm, chiều cao h = 8cm. Tính diện tích. Giải:
- S = (1/2) × a × h = 24 (cm²)
Các Lỗi Thường Gặp Và Cách Khắc Phục
Lỗi Về Công Thức
- Nhầm lẫn công thức:
- Sử dụng sai công thức cho từng trường hợp
- Áp dụng không đúng điều kiện
- Cách khắc phục:
- Ghi nhớ rõ điều kiện áp dụng
- Luyện tập nhiều dạng bài tập
Lỗi Về Tính Toán
- Sai số trong tính toán:
- Nhầm đơn vị đo
- Sai trong quá trình tính
- Giải pháp:
- Kiểm tra kỹ kết quả
- Ước lượng trước kết quả

Mẹo Học Tập Hiệu Quả
Phương Pháp Ghi Nhớ
- Liên kết kiến thức:
- Kết nối với kiến thức đã học
- Tạo sơ đồ tư duy
- Thực hành thường xuyên:
- Làm nhiều bài tập
- Đa dạng dạng bài
Cách Ôn Tập
- Hệ thống kiến thức:
- Tổng hợp công thức
- Phân loại bài tập
- Luyện tập có phương pháp:
- Từ dễ đến khó
- Đa dạng hóa bài tập
Xem thêm Cách Tính Khoảng Cách từ Điểm đến Đường Thẳng trong Hệ Tọa Độ OXYZ
Lời Khuyên Cho Phụ Huynh
Hỗ Trợ Học Tập
- Tạo môi trường học tập:
- Cung cấp tài liệu phù hợp
- Hỗ trợ khi cần thiết
- Động viên khuyến khích:
- Tạo động lực học tập
- Khen thưởng khi tiến bộ

Theo Dõi Và Đánh Giá
- Kiểm tra thường xuyên:
- Xem xét bài tập về nhà
- Đánh giá mức độ hiểu bài
- Phản hồi kịp thời:
- Góp ý xây dựng
- Điều chỉnh phương pháp học
Kết Luận
Việc nắm vững các công thức tính diện tích tam giác không chỉ giúp các em đạt kết quả tốt trong môn Toán mà còn phát triển tư duy logic và kỹ năng giải quyết vấn đề. Hy vọng bài viết này đã cung cấp cho các em và quý phụ huynh những kiến thức bổ ích về chủ đề này.
Thông tin liên hệ:
- Hotline: 0903 323 444
- Email: [email protected]
- Website: bloglamcha.com
Bài viết được đăng tải trên Blog Làm Cha – Nguồn thông tin đáng tin cậy cho phụ huynh Việt Nam. Nếu bạn thấy bài viết hữu ích, hãy chia sẻ để nhiều người cùng được biết đến những kiến thức bổ ích này nhé!
No Responses