Tọa độ vectơ là một phần quan trọng trong chương trình Toán học THPT, giúp học sinh hiểu và giải quyết các bài toán hình học trong không gian. Blog Làm Cha sẽ giúp các em nắm vững kiến thức này thông qua bài viết chi tiết dưới đây.
Khái niệm cơ bản về tọa độ vectơ
Định nghĩa tọa độ vectơ
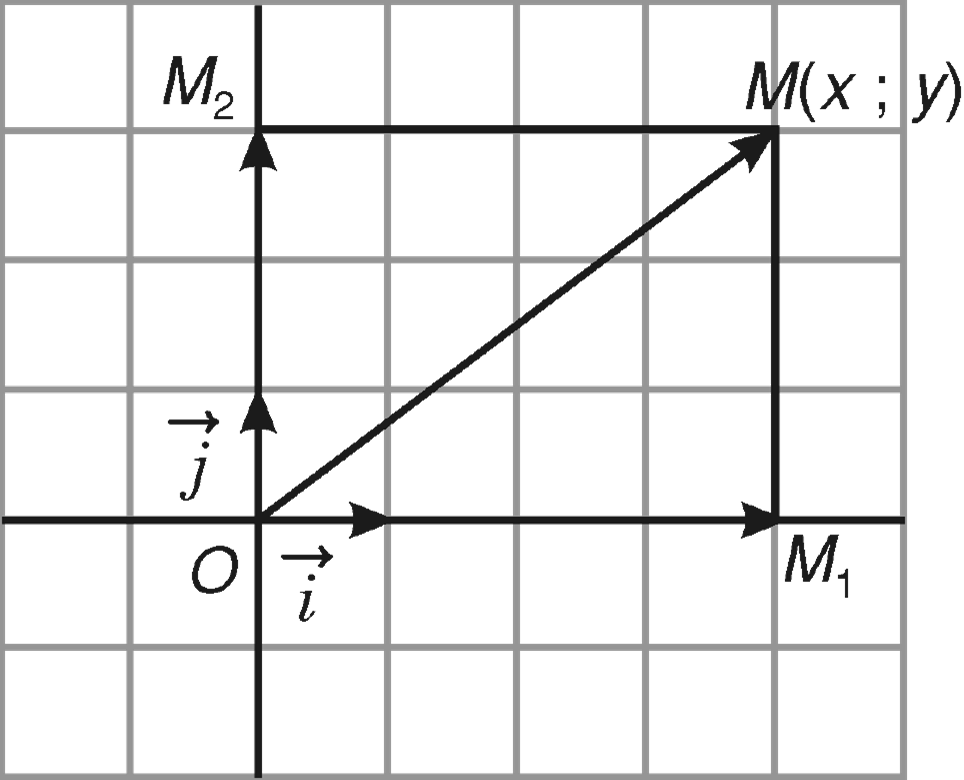
Tọa độ của một vectơ là một bộ số biểu diễn độ dời của vectơ theo các trục tọa độ. Trong không gian ba chiều, tọa độ vectơ được biểu diễn bởi ba thành phần (x, y, z), trong đó:
- x là độ dời theo trục Ox
- y là độ dời theo trục Oy
- z là độ dời theo trục Oz
Cách xác định tọa độ vectơ
- Từ điểm đầu và điểm cuối:
- Cho điểm đầu A(x₁, y₁, z₁)
- Cho điểm cuối B(x₂, y₂, z₂)
- Tọa độ vectơ AB = (x₂-x₁, y₂-y₁, z₂-z₁)
- Từ các thành phần:
- Phân tích vectơ theo các trục
- Xác định độ dời trên mỗi trục
- Ghi tọa độ theo thứ tự (x, y, z)
Các phép toán với tọa độ vectơ
Phép cộng và trừ vectơ
- Cộng hai vectơ:
a(x₁, y₁, z₁) + b(x₂, y₂, z₂) = (x₁+x₂, y₁+y₂, z₁+z₂)- Trừ hai vectơ:
a(x₁, y₁, z₁) - b(x₂, y₂, z₂) = (x₁-x₂, y₁-y₂, z₁-z₂)Phép nhân vectơ với số thực
- Công thức:
k·a(x, y, z) = (k·x, k·y, k·z)- Tính chất:
- Phân phối: k(a + b) = ka + kb
- Kết hợp: (k₁k₂)a = k₁(k₂a)
- Đơn vị: 1·a = a
Tích vô hướng của hai vectơ
Định nghĩa và tính chất
- Định nghĩa:
a·b = x₁x₂ + y₁y₂ + z₁z₂- Tính chất:
- Giao hoán: a·b = b·a
- Phân phối: a·(b + c) = a·b + a·c
- Kết hợp với phép nhân số: (ka)·b = k(a·b)
Ứng dụng của tích vô hướng
- Tính góc giữa hai vectơ:
cos φ = (a·b)/(|a|·|b|)- Kiểm tra tính vuông góc:
- Hai vectơ vuông góc khi và chỉ khi a·b = 0
Độ dài vectơ và vectơ đơn vị
Tính độ dài vectơ
- Công thức:
|a| = √(x² + y² + z²)- Tính chất:
- |ka| = |k|·|a|
- |a + b| ≤ |a| + |b|
Vectơ đơn vị
- Định nghĩa:
- Vectơ có độ dài bằng 1
- Cách tìm:
a₀ = a/|a|Ứng dụng trong hình học không gian
Phương trình đường thẳng
- Phương trình tham số:
x = x₀ + at
y = y₀ + bt
z = z₀ + ct- Véc tơ chỉ phương:
- a = (a, b, c)
Xem thêm Hình chiếu trục đo là hình biểu diễn – Hướng dẫn chi tiết cho học sinh
Phương trình mặt phẳng
- Phương trình tổng quát:
Ax + By + Cz + D = 0- Vectơ pháp tuyến:
- n = (A, B, C)
Các bài tập thường gặp
Bài tập mẫu 1: Tính độ dài vectơ
Cho vectơ a(3, 4, 0). Tính độ dài vectơ a.
Lời giải:
- Áp dụng công thức: |a| = √(x² + y² + z²)
- Thay số: |a| = √(3² + 4² + 0²) |a| = √(9 + 16 + 0) |a| = √25 = 5
Bài tập mẫu 2: Tính góc giữa hai vectơ
Cho hai vectơ a(1, 1, 0) và b(1, -1, 0). Tính góc giữa hai vectơ này.

Các lỗi thường gặp
Lỗi về tính toán
- Nhầm dấu trong phép trừ vectơ
- Sai công thức tính độ dài
- Lỗi khi tính tích vô hướng
Lỗi về khái niệm
- Nhầm lẫn giữa điểm và vectơ
- Không phân biệt vectơ chỉ phương và pháp tuyến
- Nhầm lẫn các thành phần tọa độ
Xem thêm Hướng dẫn chi tiết cách chứng minh hai đường thẳng song song lớp 7
Phương pháp học hiệu quả
Cách ghi nhớ công thức
- Hiểu ý nghĩa hình học
- Liên hệ với kiến thức cũ
- Thực hành nhiều bài tập
- Tạo sơ đồ tư duy
Cách giải bài tập
- Đọc kỹ đề bài
- Xác định dữ kiện
- Chọn công thức phù hợp
- Kiểm tra kết quả

Kết luận
Tọa độ vectơ là một công cụ quan trọng trong hình học không gian. Để nắm vững kiến thức này, các em cần:
- Hiểu rõ các khái niệm cơ bản
- Thành thạo các phép toán
- Thực hành nhiều dạng bài tập
- Liên hệ với thực tế
Để được hỗ trợ thêm về tọa độ vectơ cũng như các kiến thức Toán học khác, phụ huynh và học sinh có thể liên hệ với Blog Làm Cha qua:
- Hotline: 0903 323 444
- Email: [email protected]
- Website: bloglamcha.com
Blog Làm Cha luôn sẵn sàng đồng hành cùng các em trong việc học tập và phát triển kiến thức toán học.
No Responses